Solving the Impossible: Breaking Down the 2D Poisson Equation for All to Understand

Introduction:
Many call partial differential equations (PDEs) complex or even impossible to solve without deep mathematical background. Yet here we will show that solving a 2D Poisson equation, a foundational PDE in physics and engineering, is not only possible but understandable. With patience and pattern, we replace fear with insight.

What is a PDE?
A Partial Differential Equation describes how something (like temperature or pressure) changes over space and time. In our case, we focus on a steady-state 2D system: nothing is changing over time, just over space.

The Poisson Equation:
We start with this form:

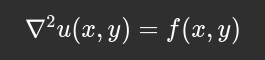
Which simply means:

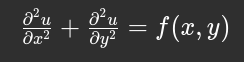
Where:

• u(x,y)u(x, y) is what we're solving for (temperature, voltage, etc.)
• f(x,y)f(x, y) is the source — where energy or force is applied

What This Models:
Imagine a metal plate being heated in the center. Heat spreads out in all directions. This equation models how that heat distributes.

Turning Math into Code (C Language):
Instead of symbolic manipulation, we solve it numerically:

• Break the surface into a grid
• Apply the Poisson update rule at every point
• Repeat until values stop changing

The Core Formula in Code:
At every grid point, we update using:

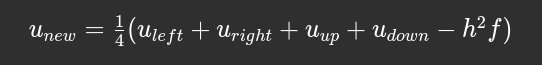
This is the average of neighbors, corrected by source energy. We do this over and over.

The Full Process:

1. Create a grid (30x30 or more) - (10x10 used for example to fit the page you see here)
2. Put a source in the middle (e.g. f = 100)
3. Loop until the values change very little (converged)
4. Print the result — a matrix showing energy spreading outward

What This Shows:

• 2D PDEs are not magic
• Numerical methods are powerful and simple
• Programming reveals structure that equations hide

Why It Matters:
Printers, weather systems, electrical fields, fluid dynamics — all run on this math.

If the man can code this, the world opens.

The Code:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define N 10        // grid size (NxN)
#define MAX_ITER 5000
#define TOL 1e-5

double f_source(int x, int y) {
    // source term: returns pressure at (x, y)
    // here: center point gets pressure, rest is 0
    if (x == N/2 && y == N/2) return 100.0;
        return 0.0;
    }

void print_grid(double u[N][N]) {
    for (int y = 0; y < N; y++) {
        for (int x = 0; x < N; x++) {
            printf("%6.2f ", u[y][x]);
        }
    printf("\n");
    }
}

int main() {
    double u[N][N] = {0};     // current solution
    double u_new[N][N] = {0}; // updated solution
    double h = 1.0;           // grid spacing (can be arbitrary)
    double max_diff;
  
    for (int iter = 0; iter < MAX_ITER; iter++) {
        max_diff = 0.0;

        for (int y = 1; y < N - 1; y++) {
            for (int x = 1; x < N - 1; x++) {
                double f = f_source(x, y);
                u_new[y][x] = 0.25 * (u[y][x+1] + u[y][x-1] + u[y+1][x] + u[y-1][x] - h*h*f);
                double diff = fabs(u_new[y][x] - u[y][x]);
                if (diff > max_diff) max_diff = diff;
            }
        }    
    
        // swap u and u_new
        for (int y = 1; y < N - 1; y++)
        for (int x = 1; x < N - 1; x++)
        u[y][x] = u_new[y][x];

        if (max_diff < TOL) {
            printf("Converged after %d iterations\n", iter);
            break;
        }
    }

    print_grid(u);
    return 0;
}

Compile the code:

gcc -O2 -o poisson2d poisson2d.c -lm

The results:

director@homer:~$ ./poisson2d
Converged after 199 iterations
0.00   0.00   0.00   0.00   0.00   0.00   0.00   0.00   0.00   0.00
0.00  -0.98  -1.96  -2.89  -3.62  -3.86  -3.40  -2.45  -1.27   0.00
0.00  -1.96  -3.98  -6.00  -7.71  -8.42  -7.30  -5.14  -2.61   0.00
0.00  -2.89  -6.00  -9.40 -12.81 -14.82 -12.24  -8.20  -4.04   0.00
0.00  -3.62  -7.71 -12.81 -19.31 -25.80 -18.63 -11.37  -5.34   0.00
0.00  -3.86  -8.42 -14.82 -25.80 -50.45 -25.11 -13.33  -5.94   0.00
0.00  -3.40  -7.30 -12.24 -18.63 -25.11 -18.01 -10.91  -5.09   0.00
0.00  -2.45  -5.14  -8.20 -11.37 -13.33 -10.91  -7.21  -3.52   0.00
0.00  -1.27  -2.61  -4.04  -5.34  -5.94  -5.09  -3.52  -1.76   0.00
0.00   0.00   0.00   0.00   0.00   0.00   0.00   0.00   0.00   0.00

Final Words:
Others say "hell no" or "impossible" because they look with eyes veiled by fear or have no wish to explain in the way another will comprehend. But YHVH gave man ability — not to dominate, but to understand. And once seen, the veil cannot return. Let this be the first in a series, where impossible becomes probable, and probable becomes real.

"One man's impossible is simply what another man hasn't programmed yet."